Use the solver in Excel to find the combination of capital investments that maximizes the total profit.
Formulate the Model
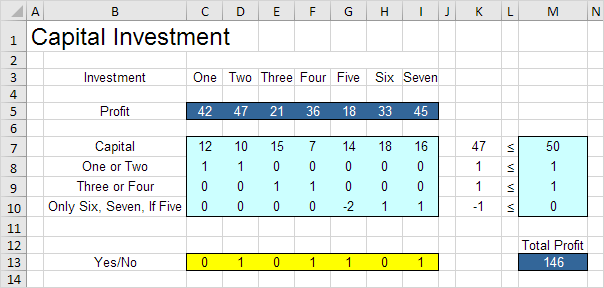
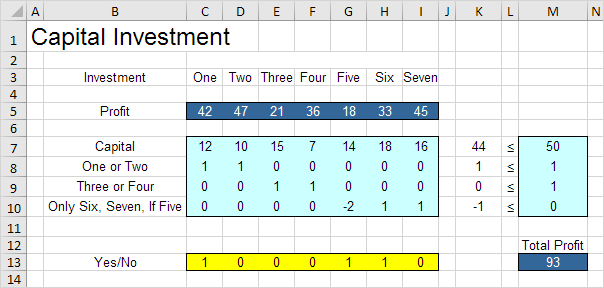
The model we are going to solve looks as follows in Excel.
1. To formulate this binary integer programming (BIP) model, answer the following three questions.
a. What are the decisions to be made? For this problem, we need Excel to find out which capital investments to make (Yes=1, No=0).
b. What are the constraints on these decisions? First, the amount of capital used by the investments cannot exceed the limited amount of capital available (50). For example, investment One uses 12 units of capital. Second, only investment One or investment Two can be made. Third, only investment Three or investment Four can be made. Fourth, investment Six and investment Seven can only be made if investment Five is made.
c. What is the overall measure of performance for these decisions? The overall measure of performance is the total profit of the capital investments made, so the objective is to maximize this quantity.
2. To make the model easier to understand, name the following ranges.
3. Insert the following five SUMPRODUCT functions.
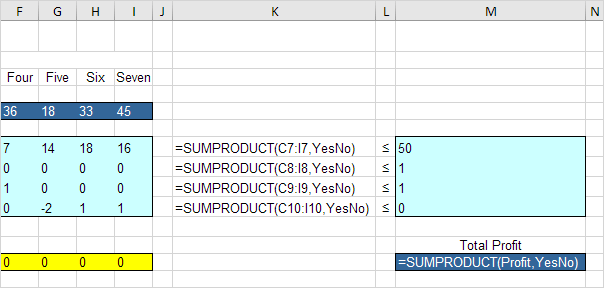
Explanation: cell K7 (the amount of capital used) equals the sumproduct of the range C7:I7 and YesNo, cell K8 equals the sumproduct of the range C8:I8 and YesNo, etc. Total Profit equals the sumproduct of Profit and YesNo.
Trial and Error
With this formulation, it becomes easy to analyze any trial solution.
1. For example, if we make investment One and Two, the second constraint is violated.

2. For example, if we make investment Six and Seven, without making investment Five, the fourth constraint is violated.
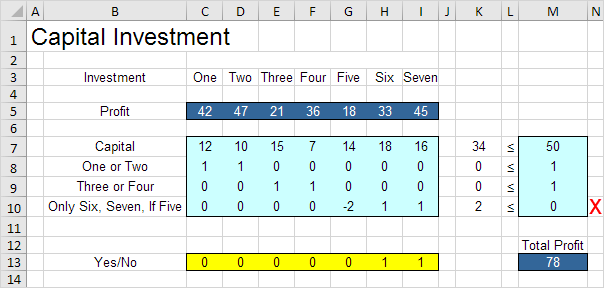
3. However, it's OK to make investment One, Five and Six. All constraints are satisfied.
It is not necessary to use trial and error. We shall describe next how the Excel Solver can be used to quickly find the optimal solution.
Solve the Model
To find the optimal solution, execute the following steps.
1. On the Data tab, in the Analyze group, click Solver.
Note: can't find the Solver button? Click here to load the Solver add-in.
Enter the solver parameters (read on). The result should be consistent with the picture below.

2. Enter TotalProfit for the Objective.
3. Click Max.
4. Enter YesNo for the Changing Variable Cells.
5. Click Add to enter the following constraint.
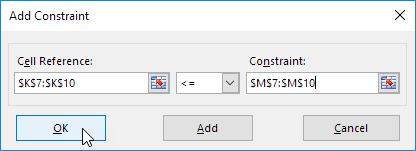
6. Click Add to enter the following constraint.
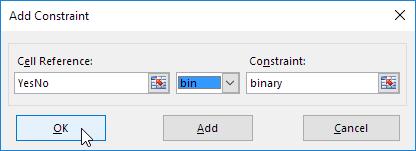
Note: binary variables are either 0 or 1.
7. Check ‘Make Unconstrained Variables Non-Negative’ and select ‘Simplex LP’.
8. Finally, click Solve.
Result:
The optimal solution:

Conclusion: it is optimal to make investments Two, Four, Five and Seven. This solution gives the maximum profit of 146. All constraints are satisfied.
