Below we will look at a program in Excel VBA that solves a small instance of a knapsack problem.
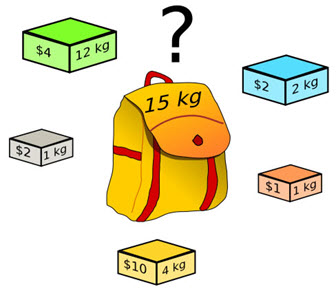
Definition: Given a set of items, each with a weight and a value, determine the items to include in a collection so that the total value is as large as possible and the total weight is less than a given limit. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most useful items.
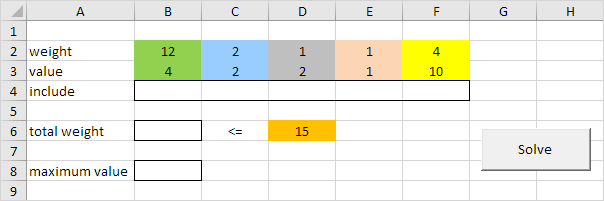
Example: 5 items with weights, values and limit as given.
In Excel this problem looks as follows:

1. First, we declare five variables of type Double with names limit, weight, value, totalWeight and maximumValue.
Dim limit As Double, weight As Double, value As Double, totalWeight As Double, maximumValue As Double
2. Next, we declare five variables of type Integer with with names i, j, k, l, m.
Dim i, j, k, l, m As Integer
3. We initialize two variables. We initialize the variable limit with the value of cell D6. We initialize the variable maximumValue with value 0.
limit = Range("D6").value
maximumValue = 0
4. Next, we check each possible solution. We can either include an item (1) or leave it out (0). We start 5 For Next loops. One for each item.
For i = 0 To 1
For j = 0 To 1
For k = 0 To 1
For l = 0 To 1
For m = 0 To 1
5. We calculate the weight and the value of a possible solution.
weight = 12 * i + 2 * j + 1 * k + 1 * l + 4 * m
value = 4 * i + 2 * j + 2 * k + 1 * l + 10 * m
6. Only if value is higher than maximumValue and weight is lower than limit, we've found a new better solution.
If value > maximumValue And weight <= limit Then
7. If true, we write the new solution to row 4, weight to totalWeight and value to maximumValue.
Range("B4").value = i
Range("C4").value = j
Range("D4").value = k
Range("E4").value = l
Range("F4").value = m
totalWeight = weight
maximumValue = value
8. Don't forget to close the If statement.
End If
9. Don't forget to close the 5 For Next loops.
Next m
Next l
Next k
Next j
Next i
Excel VBA checks each possible solution this way and as a result the optimal solution will appear in row 4. Remember, 1 means we include an item, 0 means we leave it out.
10. Finally, write totalWeight and maximumValue of the optimal solution to respectively cell B6 and B8.
Range("B6").value = totalWeight
Range("B8").value = maximumValue
11. Test the program.
Result:
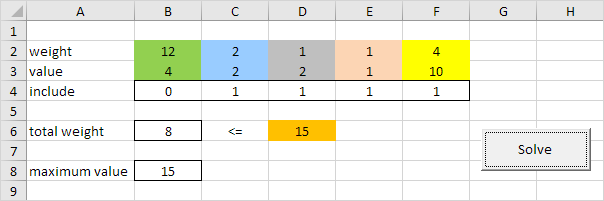
Conclusion: it's optimal to include the last four items with a maximum value of 15. This solution with a total weight of 2 + 1 + 1 + 4 = 8 does not exceed the limit of 15.
Note: by making the weights and values variable you can solve any knapsack problem of this size (see downloadable Excel file).
