The kth term, Tk, of a certain mathematical series is defined by the following formula:
| Tk | = | k2 + 6k + 1 |
| 9k + 7 |
The first term, T1, of the series is obtained by substituting k = 1 into the formula i.e.
| T1 | = | 12 + 6 + 1 | = | 1 | and |
| 9 + 7 | 2 |
| T2 | = | 22 + 12 + 1 | = | 17 | ... and so on |
| 18 + 7 | 25 |
Below we will look at a program in Excel VBA that calculates any term Tk and summation of terms up to N.

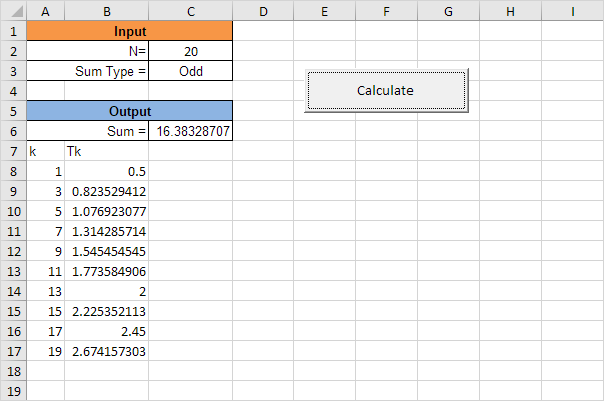
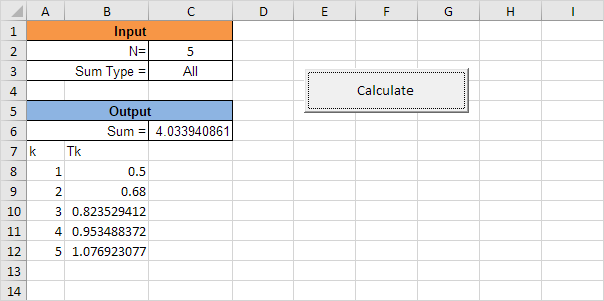
Explanation: the user has the option to enter “All” or “Odd”, to respectively calculate the sum of the first N terms of the series or the sum of only the odd terms up to N.
Place a command button on your worksheet and add the following code lines:
1. First, we declare four variables of type Integer and one variable of type String.
Dim i, term, N, stepSize As Integer
Dim sumType As String
2. Second, we initialize the variables.
i = 0
N = Range(“C2”).Value
sumType = Range(“C3”).Value
3. Empty the fields.
Range(“A8:B1000”).Value = "”
Range(“C6”).Value = "”
4. Determine stepSize.
Select Case sumType
Case Is = “All”
stepSize = 1
Case Is = “Odd”
stepSize = 2
Case Else
MsgBox “Enter a valid expression in cell C3”
End
End Select
Tip: go through our Select Case program to learn more about the Select Case structure.
5. Do the calculations.
For term = 1 To N Step stepSize
Cells(8 + i, 1).Value = term
Cells(8 + i, 2).Value = (term ^ 2 + (6 * term) + 1) / ((9 * term) + 7)
Range(“C6”).Value = Range(“C6”).Value + Cells(8 + i, 2).Value
i = i + 1
Next term
Explanation: we use the Step keyword to specify the increment (1 for “All” and 2 for “Odd”) for the counter variable of the loop.
Result: